Tree

Tree/Pohon

Pada struktur data kita juga mempelajari tree/pohon seperti juga pada mata kuliah Matematika Diskrit, bedanya ya tentu saja pada mata kuliah Struktur Data kita membuat code nya.
Nah, sebelum berbicara lebih jauh, berikut merupakan beberapa konsep yang harus di ketahui mengenai tree :

1. Tree adalah kumpulan beberapa node.
2. Node yang paling atas yang tidak memiliki parent disebut dengan akar/root.
3. Sebuah garis yang menghubungkan parent dengan anaknya disebut dengan edge.
4. Node yang tidak memiliki anak disebut dengan leaf/daun.
5. Node-node yang memiliki orang tua yang sama, berarti node-node tersebut bisa dikatakan saudara/sibling.
6. Degree sebuah node adalah total subtree node.
7. Height/Depth adalah ketnggian dari suatu pohon.

Binary Tree

Dapat diartikan sebagai tree yang setiap node nya paling banyak memiliki 2 anak.,left child dan juga right child.

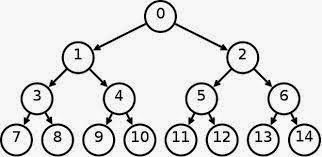
Nah pada gambar diatas merupakan contoh dari binary tree.

Root/akar dari tree tersebut adalah angka 2 paling atas yang tidak memiliki parent, dan yang merupakan leaf/daun adalah angka 2 yang dibawah,5,11,4.

Macam-macam Binary Tree

1. Perfect Binary Tree : tree yang setiap node nya pasti memiliki 2 anak sehingga tree tersebut menjadi seimbang bagian kiri maupun kanan nya. Berikut ini merupakan contoh nya :
   
2. Complete Binary Tree : tree yang notabene lebih condong kekiri dikarenakan cara pengisian setiap level nya dengan cara bagian kiri diisi terlebih dahulu. Perfect Bianry Tree juga termasuk kedalam Complete Binary Tree. Berikut ini merupakan contoh nya :
   
3. Skewed Binary Tree : tree dimana node-node hanya memilki satu anak sehingga tree akan condong/berat sebelah, bisa kekiri maupun kekanan. Berikut ini merupakan contoh nya :
   

Hal-hal mengenai binary Tree :

1. Jumlah maksimum node disuatu level k pada binary tree yaitu 2k. Dimana level pada binary tree dimulai dari level 0.
2. Jumlah maksimum semua node pada ketinggian h pada binary tree yaitu 2h+1 - 1, dimana ketinggian dimulai dari 0.
3. Ketinggian minimum dari suatu binary tree yang memiliki node sebanyak n yaitu 2log(n).
4. Ketinggian maksimum dari suatu binary tree yang memiliki node sebanyak n yaitu n-1.(pada skewed binary tree).

Tree sendiri kemungkinan akan digunakan / sangat berhubungan dengan prefix,infix dan juga postfix

Contoh : prefix +ab

infix a+b

postfix ab+

Binary Seach Tree

adalah binary tree dengan tambahan-tambahan sebagai berikut :

1. Setiap node memiliki sebuah key/kunci dan tidak ada node lain yang memiliki key yang sama.
2. Node-node yang berada di sebelah kiri root memiliki key yang lebih kecil dibandingkan dengan key di root(standar nya seperti itu, tapi bisa juga sebaliknya).
3. Node-node yang berada di sebelah kanan root memiliki key yang lebih besar dibandingkan dengan key di root(standar nya seperti itu, tapi bisa juga sebaliknya).

Berikut merupakan contoh Binary Search Tree 

Kegunaan utama dari BST sendiri yaitu memudahkan dan juga mempercepat dalam mencari data hingga mencapai 2x lebih cepat. Itulah mengapa skewed tree dapat dilakukan AVL agar tree jadi seimbang dan mempercepat pencarian data.

Berikut ini merupakan 3 operasi pada BST :

1. Searching/Pencarian
1. Langkah :
1. Dimulai dari root.
2. Jika data di root sama dengan data yang ingin dicari maka proses pencarian selesai.
3. Jika key yang ingin dicari < data di root maka cari secara rekursif pada subtree yang kiri dan bila key > data di root maka cari secara rekursif pada subtree kanan.
2. Insert/Memasukkan data
1. Langkah:
1. Dimulai dari root.
2. Jika data yang ingin dimasukkan < data di root maka masukkan data tersebut ke subtree kiri dan lakukan terus menerus secara rekursif, sebaliknya jika data yang ingin dimasukkan > data di root maka masukkan data tersebut ke subtree kana dan lakukan juga terus menerus secara rekursif.
3. Lakukan terus sampai ditemukan node kosong untuk meletakkan data tersebut(data yang di masukkan akan selalu menjadi leaf/daun).
3. Delete/Menghapus node
1. Langkah :
1. Jika key nya di daun maka lagsung hapus saja node tersebut.
2. Jika key nya pada node yang memiliki 1 anak/child maka hapus node tersebut dan hubungkan childnya dengan parentnya–If the key is in a node which has one child, delete that node and connect its child to its parent
3. Jika key nya pada node yang memiliki 2 anak, temukan child yang paling kanan dari subtree kiri dan lakukan secara rekursif.
4. 
   
5. Operasi delete pada BST merupakan operasi tersulit dalam melakukan coding nya diantara operasi lainnya.

Preorder
Preorder adalah cara untuk menampilkan data dengan urutan seperti prefix. Rumus untuk preorder adalah PLR, yaitu data yang ditemukan(ditengah) dicetak/print (Print), kemudian bergerak kesebelah kiri (Left), setelah itu kesebelah kanan (Right).


Inorder
Inorder adalah cara untuk menampilkan data dengan urutan seperti infix. Rumus untuk inorder adalah LPR, yaitu memproses data disebelah kiri (Left),data yang ditemukan(ditengah) diprint (Print), lalu bergerak kesebelah kanan (Right).

Postorder
Postorder adalah cara untuk menampilkan data dengan urutan seperti postfix. Rumus untuk postfix adalah LRP, yaitu memproses data disebelah kiri (Left), kemudian bergerak kesebelah kanan (Right). terakhir baru memprint data yang ditemukan(ditengah) (Print).

NB : Bahan yang ditulis berdasarkan apa yang pernah saya pelajari dari dosen dan juga slide-slide powerpoint dari Binus University.


Binus University     Skyconnectiva