Balanced Binary Tree

Balanced Binary Tree

Pada bahasan ini, dipelajari pembuatan tree yang seimbang (tidak skewed) yang akan memudahkan kita dalam melakukan pencarian data (pencarian data menjadi lebih cepat), karena membuat sebuah tree height nya menjadi lebih kecil, sehingga worst case (tinggi tree) nya menjadi  θ(log n), tidak θ(n).

Untuk membuat tree menjadi seimbang dapat dilakukan dengan cara AVL tree atau pun RBT tree

Contoh pada AVL:

Contoh pada RBT:

Penjelasan lebih lanjut mengenai balanced binary tree akan dijelaskan pada bagian AVL dan juga RBT.

B Tree

B-Tree

Pohon sebanyak M-cara yang dibuat oleh Rudolf Bayer dan Ed McCreight yang digunakan secara luas untuk mengakses disk. Sebuah B-Tree dengan orde M, dapat mempuyai key sebanyak M-1, dan pointer sebanyak M ke sub-tree. B-Tree dirancang untuk menyimpan data terurut dan memungkinkan untuk searching, insertion, dan deletion.

Konsep nya mirip sama 2-3 tree beda nya kalo 2-3 tree itu b-tree dengan orde 3, sedangkan b-tree itu ordenya  bebas.

Contoh B-Tree:

*B-tree dengan order 5

Ketentuan B-Tree:

a.       Jika B-Tree order n:

a.       Tiap node maksimal bisa punya n anak.

b.      Tiap node minimal punya n/2 anak.

c.       Root min punya 2 anak.

d.      Semua leaf berada di level yang sama.

e.      Data disusun berdasar sorted order.

f.        Node maks punya n-1 data.

Operasi-operasi pada B-Tree:

a.       Insert:

a.       Jika jmlh data di leaf<order-1, maka masukkin data nya disitu.

b.      Jika sudah full, maka push middle data nya dan split/pisah jadi 2 node yaitu data-data dikiri middle data dan data-data di kanan middle data.

b.      Delete:

a.       Jika jumlah data di node nya>order/2, maka delete saja.

b.      Jika jumlah data di node nya<=order/2:

                                                               i.      Jika jumlah data di node sibling nya>order/2 maka lakukan rotasi.

                                                             ii.      Jika jumlah data di node siblingnya<=order/2 maka lakukan turun dan merge.

                                                            iii.      Lakukan seterusnya.

Leftist Tree, Tries dan Hashing

Leftist Tree

Merupakan tree perpanjangan dari extended Binary Tree, dimana external node pada extended Binary Tree akan digunakan untuk menghitung jarak yang nantinya akan berguna saat melakukan operasi” pada leftist tree.

s(x) merupakan jarak antara node tersebut dengan extended binary tree terdekat.

Contoh:

Angka berwarna biru merupakan nilai s(x) nya.

Operasi-operasi pada Leftist Tree:

·         Combine

o   Berarti menggabungkan 2 tree menjadi 1.

o   Cara:

§  Misal kan ada 2 tree yg ingin dicombine, maka compare root pada kedua tree tsb, yg root nya lbh kecil jadi root, lalu compare root yg tadi lbh besar dengan anak kanan dr root tree baru, dst.

·         Insert

o   Menggunakan konsep combine juga.

o   Node baru yg diinsert itu selalu menjadi tree baru terlebih dahulu sebelum diinsert ke tree.

o   Node baru akan menjadi anak kanan dari root.

o   Hitung s(x) nya dimana s(x) di anak kiri harus>=s(x)di anak kanan, bila tidak maka diswap antara anak kiri dan anak kanan.

·         Delete

o   Yang bisa di delete hanya rootnya saja spt heap,deap.

o   Setelah  root didelete maka aka nada 2 tree yaitu tree yang sebelumnya menjadi right subtree dr root dan juga yang tadinya menjadi left subtree dari root.

o   Maka lakukan kembali proses combine.

Tries

Bukan lah sebuah tree karena memiliki banyak sekali cabang.

Kata trie berasal dari kata retrieval, sesuai dengan kegunaannya.

Digunakan dalam search engine, missal ketika kita mengetik a, maka pada search engine akan ada suggestion seperti ayam,adi ,dst.

Operasi pada Tries:

·         Insert:

o   Yang lebih besar akan menjadi anak kanan, sehingga semakin besar huruf awal(ascii) semakin ke kanan.

o   Kalo masukkin data yang awal”nya sama missal bar sama barang, awalnya sama-sama bar, maka Pada huruf r dikasih lambang sebagai penanda bahwa ada kaga bar jg.

·         Delete:

o   Kalo data nya unik/ga ada cabang maka hapus saja.

o   Kalau key merupakan awalan spt cth tadi bar dan barang maka pada huruf r lambing nya hapus saja.

o   Kalau key merupakan cabang, maka hapus lah cabang nya.

 Contoh tries:

Hashing

Hash table adalah sebuah table array dimana kita menyimpan data.

Biasanya ukuran hash table lebih keccil dibandingkan dengan kemunkinan string yang diinsert,sehingga bisa / ada kemunkinan terjaidinya hased key yang sama.

Hash table terdiri dari array nya missal a[], dan juga value/ data nya.

Ada beberapa cara untuk menentukkan string ini dimasukkna kemana, dst.

1.       Mid-square

a.       String nya(ascii) dikuadratkan, kemudian ambil nilai tengah(bisa 1 data, 2 data, dst), nah hasilnya akan dihjadikkan tempat dimana data tsb diletakkan.

2.       Division:

a.       String nya(ascii) dimoduluskan dengan sebuah angka(lbh baik bilangan prima agar hasilnya random dan unik), nah hasilnya menjadi tempat peletakkan string tersebut.

3.       Folding:

a.       String nya diubah jadi ascii kemudian ascii dari masing masing huruf ditambahkan antara satu dan yang lainnya, dan hasilnya dijadikan hash key (tempat peletakkan string nya).

Delete pada Hash table walaupun setelah di delete dan ternyata data kosong, maka ga bleh dikoongn begitu saja, tetap harus di kasih tanda bahwasanya array tersebut sebelumnya  pernah keisi.

Collision adalah suatu kondisi dimana ada string lain nya yang ditempatkan di tempat yang sudah ada string nya.

Cara mengatasi nya:

1.       Linear probing: sehingga jika terjadi collision maka string yang baru tersebut ditaruh di array setelahnya yang masih kosong, tapi cara ini memiliki kelemehan terlebih ketika array nya penuh maka tidak ada cara lagi, makanya lebih baik memakai cara yang kedua.

2.       Chaining, sehingga dengan cara ini jika terjadi collision pada array dibuat linked list, sehingga sulit untuk kehabisan array dengan cara linked list ini sehingga cara ini lebih baik digunakan dibandingkan dengan liear probing, contoh : a[0] : adi->alam->agar

Deap

Deap

Deap (Double ended heap) mirip dengan Min-Max Heap. Bedanya, bila min-max heap, min dan max nya selang seling atas bawah maka pada deap min di kiri dan max ada di kanan.

Contoh deap:

Jadi pada deap:

• Root nya blank(null)
• Left subtree dari root berisi min heap
• Right subtree dari root berisi max heap

Partner adalah node yang berada di posisi yang sama bila subtree min-heap dan max-heap ditumpuk menjadi 1. Contoh:

Jika partner tidak ada maka yang dianggap partner adalah partner dari node yang seharusnya menjadi partner, seperti partner node 9 merupakan 40.Partner dari 10 adalah 25, partner dari 40 merupakan 8,9 dan 30.

Untuk mencari lokasi partnernya :

•       Min-partner -> x-x/2

•       Max-partner -> x+x/2

•       Jika lokasi partnernya kosong, maka partnernya menjadi parent dari posisi partner yang seharusnya.

•       Parent min partner -> (x-x/2)/2

•       Parent max partner -> (x+x/2)/2

Cara insert deap:

•       Node baru masuk di index terakhir.

•       Periksa kondisi pada elemen partner :

                - Jika insert pada min-heap tetapi nilainya lebih besar dari max-partner maka tukar.

                - Jika insert pada max-heap tetapi nilainya lebih kecil dari min-partner maka tukar.

•       Lakukan Min-upHeap atau Max-upHeap berdasarkan lokasi elemen baru.

Cara delete deap:

•       Ada 2 jenis : delete min dan delete max.

•       Jika delete min, maka yang dihapus adalah root dari min-heap. Jika delete max, maka yang dihapus adalah root dari max-heap.

•       Setelah dihapus, seperti biasa, elemen terakhir dari heap menggantikan posisi dari yang terhapus, kemudian di-downheap. Bedanya dengan heap biasa adalah setelah di-downheap, maka akan dilakukan pengecekan terhadap partner.

Heap

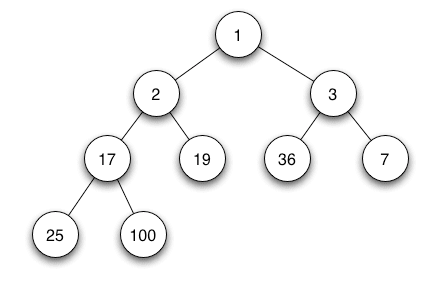
Heap

Merupakan sebuah complete binary tree

Diimplementasikan menggunakan array atau linked list. Heap konsep nya sama seperti priority queue.

Kegunaan heap adalah untuk mencari elemen terkecil(min heap)/elemen terbesar(max heap)

Heap ada beberapa jenis, yaitu:

1.       Min heap : root nya merupakan elemen terkecil, dan semakin kebawah data nya semakin besar

        Contoh:

2.       Max heap : root nya merupakan elemen terbesar dan semakin ke bawah data nya semakin besar.

       Contoh:

3.       Min-Max heap : heap yang tiap level nya berselang seling min – max – min – max – dst.

        COntoh:

Min Heap & Max Heap

Cara insert:

a.       Jika min heap(elemen terkecil terletak di root):

a.       Masukkan data nya tidak seperti BST , melainkan dengan konsep array, sehingga kekanan terus, lalu kebawah, dst, atau bisa dikatakan bahwa elemen terakhir akan masuk ke index terakhir/menjadi anak paling kanan dan bawah.

b.      Data yang diinsert kemudian dibandingkan dengan parentnya, jika lbh kecil maka swap, lakukan terus menerus sampai root atau sampai data baru tersebut lbh besar dr parentnya.

b.      Jika max heap(elemen terbesar terletak di root):

a.       Masukkan data nya tidak seperti BST , melainkan dengan konsep array, sehingga kekanan terus, lalu kebawah, dst, atau bisa dikatakan bahwa elemen terakhir akan masukk ke index terakhir/menjadi anak paling kanan dan bawah.

b.      Data yang diinsert kemudian dibandingkan dengan parentnya, jika lbh besar maka swap, lakukan terus menerus sampai root atau sampai data baru tersebut lbh kecil dr parentnya.

c.       Implementasi dengan array, root itu index nya 1, bukan 0.

Perhitungan:

a.       Parent(x)             = x / 2

b.      Left-child(x)       = 2 * x

c.       Right-child(x)     = 2 * x + 1

    

Cara delete:

a.       Jika min heap(elemen terkecil terletak di root):

a.       Maka yang dihapus merupakan rootnya(elemen terkecil).

b.      Root yang dihapus tersebut kemudian digantikan oleh data terakhir di nodenya, kemudian data tersebut di downheapmin(jika anak < data tsb, maka tukar,dst sampai mentok dibawah atau node tsb<anaknya).

b.      Jika max heap(elemen terkecil terletak di root):

a.       Maka yang dihapus merupakan rootnya(elemen terbesar).

b.      Root yang dihapus tersebut kemudian digantikan oleh data terakhir di nodenya, kemudian data tersebut di downheapmax(jika anak > data tsb, maka tukar,dst), sampai mentok dibawah atau node tsb>anaknya).

Min-Max Heap

•       Min-Max Heap adalah kombinasi dari min heap dan max heap.

•       Masing-masing level akan berganti-ganti antara min heap dan max heap, diawali dengan min heap.

•       Heap ini berguna untuk langsung menemukan nilai min dan nilai max dalam 1 heap saja.

•       Kekurangannya heap jenis ini menemukan 1 nilai min dan 2 nilai max.

•       Pada level min semakin ke bawah nilainya semakin besar.

•       Pada level max semakin ke bawah nilainya semakin kecil.

Insert Min-Max Heap:

a.       Insert di level Min:

-          Proses Node baru yang akan dilakukan dipengaruhi oleh lokasi Node baru tersebut.

-          Jika Node baru berada di level min, maka bandingkan dengan parentnya.

                                                               i.      Jika parent < newnode maka swap dan upheapmax dari parentnya (dibandingkan dengan grandparentnya dari posisi newnode setelah swap).

                                                             ii.      Jika parent > newnode, upheapmin dari posisi newnode (dibandingkan dengan grandparentnya dari posisi newnode).

b.      Insert di Level Max:

-          Proses Node baru yang akan dilakukan dipengaruhi oleh lokasi Node baru tersebut.

-          Jika Node baru berada di level max, maka bandingkan dengan parentnya.

                                                               i.      Jika parent > newnode maka swap dan upheapmin dari parentnya (dibandingkan dengan grandparentnya dari posisi newnode setelah swap).

                                                             ii.      Jika parent < newnode, upheapmax dari posisi newnode (dibandingkan dengan grandparentnya dari posisi newnode).

Deletion pada min-max heap bisa min nya atau max nya.

Cara delete:

a.       Nilai yang dihapus diganti oleh data terakhir.

b.      Komparasi dengan grandchild baru lakukan komparasi dengan child nya terus menerus.